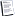No, you're absolutely correct. You should not accept the bet. The reason is inclusion-exclusion. What we're really doing is looking at the second deck as a permutation (shuffling) of the first, and asking if there are any fixed points. Let N(i) be the number of shufflings in which the i'th cards are identical. We want to know how many shufflings there are where this never happens for any i.


Suppose our deck has n cards, so here n = 52. Let N(i,j,k) be the number of shufflings where the i'th, j'th, and k'th cards are identical, and so on.


N(i) = (n-1)!, because there are (n-1)! ways to permute the remaining cards.


N(i,j) = (n-2)!, because there are (n-2)! ways to permute the remaining cards.


And so on.


Also, when we apply inclusion-exclusion, there are C(n,1) terms of type N(i), C(n,2) terms of type N(i,j), etc. In general, there are C(n,k) terms corresponding to shufflings which have k identical cards.


Thus, the number of ways that none of the cards can fall identically is


n! - (n-1)!*C(n,1) + (n-2)!*C(n,2) - (n-3)!*C(n,3) + ... + (-1)^n,


the final term corresponding to k = n.


Now, if we divide this by n!, we get that


1 - 1/(1!) + 1/(2!) - 1/(3!) + 1/(4!) - ... + (-1)^n/(n!)


is the probability that none of the cards will fall identically.


This is the series expansion of e^x, where x = -1. So, the above expansion is just a partial sum approximation for 1/e. This means the probability that at least one of the cards WILL fall identically is (e-1)/e, and so the odds for the bet should be set at (e-1):1, which is about 1.718:1. This is why both 3:2 and 5:3 are losing bets.